Ein Modell zum Abbremsen schwerer Ionen
Neue Vorhersagen über die Kollision von schweren Ionen bei sehr hohen relativistischen Energien.
Kernphysik
Fusionsforschung – Quo vadis?
Das neue Physikkonkret der DPG nimmt die Fortschritte der Fusionsforschung ins Visier.
Wie Kernphysik die Vorhersage von Erdbeben verbessern kann
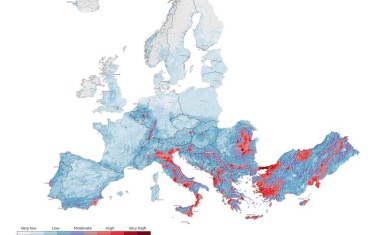
Sensor-Netz soll den Radongehalt in europäischen Wasserquellen messen.
02.03.2023 • Nachricht • Industrie & Technologie
Einzelmolekül-MRT durch Quantensensoren
Mit Atomen dicht unter der Diamant-Oberfläche wollen Forscher einzelne Zellen und einzelne Moleküle ins Visier nehmen.
Der empfindlichste Detektor zur Messung von Radioaktivität
Neben der Messung von Proben kann die Anlage auch für die physikalische und astrophysikalische Grundlagenforschung genutzt werden.
Kernfusion: Wendelstein 7-X erreicht Meilenstein
Leistungsplasma mit einem Energieumsatz von 1,3 Gigajoule über acht Minuten erzeugt.
Es gibt keine sterilen Neutrinos
Finale Ergebnisse der STEREO-Kollaboration schließen Existenz des zusätzlichen Neutrino-Zustands aus.
Kernfusions-Simulation wird Vorreiter beim Übergang zu Exascale-Supercomputern
Simulationscode GENE macht digitale Zwillinge von Kernfusions-Experimenten möglich.
Neue Lösung für eines der großen Probleme der Fusionsforschung
Experimente und Simulationen zeigen, wie sich zerstörerische Plasma-Instabilitäten in Fusionsreaktoren vermeiden lassen.
Größe eines exotischen Nickel-Isotops gemessen
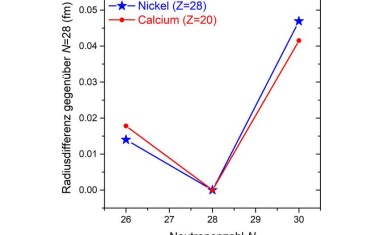
Damit lässt sich erstmals der Verlauf des Ladungsradius über einen neutronenarmen doppelt magischen Kern hinweg verfolgen.
Quantifizierung von Strahlenschäden in Materialien
Gespeicherte Energiemenge liefert Aufschluss über Zerstörungsausmaß auf atomarer Ebene.
Steiniger Weg zu den Sternen
Eine zweiteilige Serie in „Physik in unserer Zeit“ erklärt die Herkunft der Elemente durch die kosmische Nukleosynthese im Detail.
Neue Einblicke in die Physik von Neutronensternen
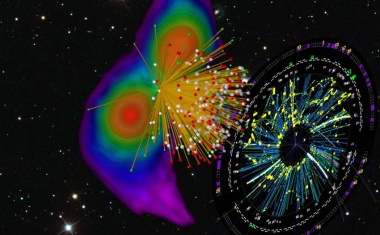
Kombination von Schwerionen-Experimenten, astrophysikalischen Beobachtungen und Kerntheorie
Wie magnetisch ist Helium-3?
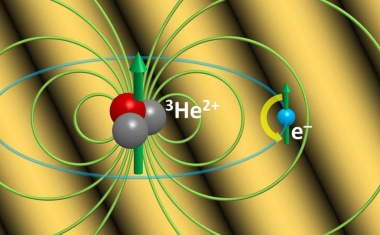
Erste direkte Kalibrierung für 3He-Kernspin-Resonanz-Sonden.
25.02.2022 • Nachricht • Industrie & Technologie
Medizinische Radioisotope bei extremer Energiedichte erzeugen
Kooperation erreicht Meilenstein mit erfolgreichem Beschleuniger-Experiment.
Paolo Giubellino bleibt wissenschaftlicher Geschäftsführer von GSI und FAIR
FAIR-Council und GSI-Aufsichtsrat konnten international renommierten Wissenschaftler für eine zweite Amtszeit gewinnen.
Ladungsradien als Prüfstein neuester Kernmodelle
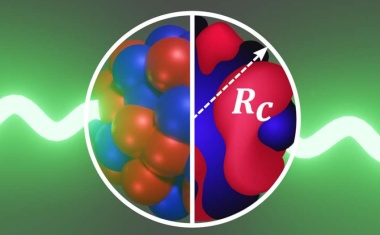
Übereinstimmung experimentellen Daten mit DFT-Ergebnissen und drei unabhängigen ab-initio-Rechnungen.
Kernfusion durch künstliche Blitze
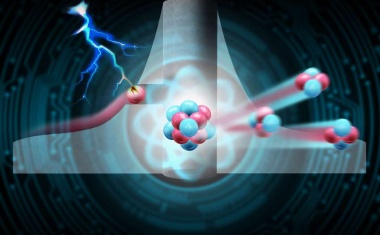
Fusionsprozesse lassen sich durch gepulste elektrische Felder anstoßen.
Gibt es Tetra-Neutronen?
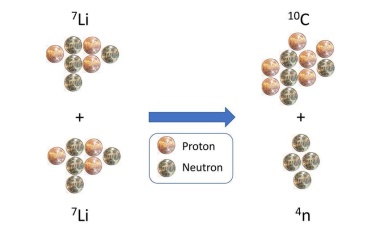
Messwerte deuten auf Existenz der lange gesuchten Teilchen aus vier Neutronen.
Leichten Teilchen der dunkle Materie auf der Spur
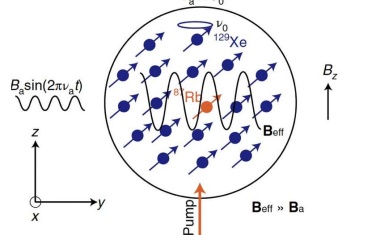
Neue Technik der kernmagnetischen Resonanz um fünf Größenordnungen empfindlicher.
Den Geheimnissen eines exotischen Kerns auf der Spur
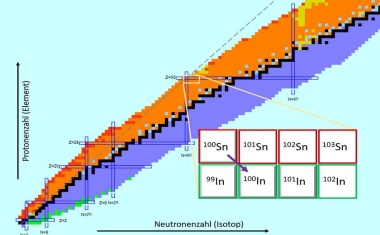
Berechnungen des experimentell schwer zugänglichen Kerns Zinn-100 mit neuesten ab-initio-Methoden liefern verlässliche Ergebnisse.
Besserer Zugang zu neuen Radionukliden
PRISMAP – ein europäisches Programm für medizinische Radionuklide.
Messmethode der Neutrinophysik auf dem Prüfstand
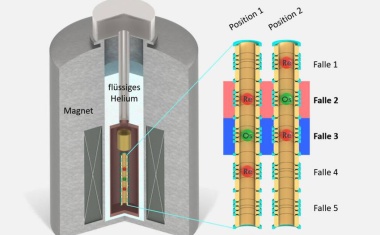
Präzisen Massenmessungen und Rechnungen überprüfen Genauigkeit der kryogenen Mikrokalorimetrie.
Wie Leptonen an Atomkernen streuen
Präzise theoretische Vorhersagen sind wichtig für künftige Neutrinoexperimente.
Das Konzept von Wendelstein 7-X bewährt sich
Teil der Optimierungsstrategie experimentell bestätigt.
Europium-Sterne in der Zwerggalaxie Fornax
Neuer Einblick in den Ursprung der Elemente gelungen.
Gemeinsam die Entstehung der Elemente ergründen
EU-Netzwerk für Forschungsinfrastrukturen in der nuklearen Astrophysik gegründet.
Atomkerne: Bruchstücke drehen sich erst nach der Spaltung
Experimente zeigen Entstehung des Spin der Fragmente eines gespaltenen Atomkerns.
Exaktere Messung des Helium-Kerns
Neue Werte ermöglichen genauere Bestimmung von Naturkonstanten.
Zentrum der Insel der Stabilität liegt nicht bei Element 114
Schwerere Elemente rücken jetzt verstärkt ins Rampenlicht.
Heliumkerne in schweren Atomkernen entdeckt
Wahrscheinlichkeit für die Bildung von Heliumkernen nimmt mit dem Neutronenüberschuss der Kerne ab.
Simulierte Nuklidkarte
Vorhersage der Eigenschaften von fast 700 Isotopen zwischen Helium und Eisen.
Europa bleibt Herrin der Ringe und Quantenoptik erhellt fortan die starke Kraft
Jahresrückblick Teilchen-, Kern- und Beschleunigerphysik 2020.
Einblicke in Extremzustände der Materie
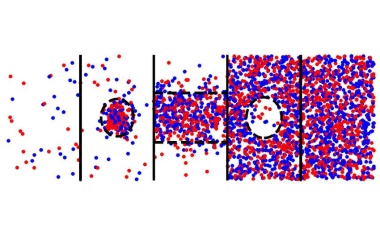
Erste exakte Berechnung des Phasenübergangs von Nukleonen.
Mit laserbeschleunigten Protonen die Astrophysik verstehen
Erstmals per Hochleistungslaser beschleunigte Protonen zur Spaltung von Atomkernen eingesetzt.