Bei der Arbeit im Homeoffice führen die fehlende Trennung von Beruf und Familie sowie die zusätzliche Belastung durch Homeschooling zu Stress, insbesondere bei Frauen (Bild: Anke Thomass / Adobe Stock, vgl. S. 24).
Ausgabe lesen

Bei der Arbeit im Homeoffice führen die fehlende Trennung von Beruf und Familie sowie die zusätzliche Belastung durch Homeschooling zu Stress, insbesondere bei Frauen (Bild: Anke Thomass / Adobe Stock, vgl. S. 24).
Das Munich Quantum Valley soll die Forschung zu Quantentechnologien vorantreiben.
Wissenschaftlerinnen und Wissenschaftler fordern eine europäische Strategie, um die Covid-19-Fallzahlen rasch und nachhaltig zu reduzieren.
Der deutsche ESA-Astronaut Matthias Maurer startet im Herbst zu seiner ISS-Mission „Cosmic Kiss“.
Am TRIUMF in Kanada haben Teile von ARIEL einen ersten wichtigen Test bestanden.
Neuer Rekordhaushalt, Mehr Geld für Grundlagen, Angewandte Kernfusion, Gegen Kernwaffentests, Wichtig oder gefährlich?
 • 2/2021 • Seite 18 • DPG-Mitglieder
• 2/2021 • Seite 18 • DPG-MitgliederPhysikalische Modelle zeigen, dass unterschiedliche Verteilungen knapper Impfdosen den Verlauf des Infektionsgeschehens deutlich beeinflussen können.
 • 2/2021 • Seite 22
• 2/2021 • Seite 22Im Interview erläutert der Strömungsphysiker Eberhard Bodenschatz, wie Aerosole entstehen und sich ausbreiten und welchen Schutz Masken bieten.
SARS-CoV-2 überträgt sich durch humane Aerosole und Tröpfchen. Am Max-Planck-Institut für Dynamik und Selbstorganisation in Göttingen führte Eberhard Bodenschatz mit seinem Team seit März 2020 Messungen an mehr als 140 Freiwilligen durch. Die Untersuchungen zeigten unter anderem, dass Gesichtsmasken einen sehr guten Schutz darstellen, dass das Spielen von Blasinstrumenten möglich, aber singen keine gute Idee ist.
Welche Faktoren spielen bei der Übertragung des Coronavirus durch Aerosole eine Rolle?
Wir atmen Tröpfchen aus, in denen sich die Virionen befinden, also die Viruspartikel, die verantwortlich sind für die Ansteckung. Die Infektion geschieht weniger durch Übertragung durch die Hand, weil wir inzwischen gelernt haben, uns regelmäßig und gründlich die Hände zu waschen. Der Hauptübertragungsweg ist derjenige über Tröpfchen. Größere Tröpfchen über 50 Mikrometer fallen irgendwann auf den Boden und trocknen. Wenn diese wieder aufgewirbelt werden, können sie allerdings wieder ansteckend wirken.
Und was ist mit den kleineren Tröpfchen?
Die bleiben sehr lange in der Luft. In den schnell trocknenden Tropfenkernen, also Aerosolen, sind im Wesentlichen Salz, Proteine und hier und da ein Virus. Die Ansteckungswahrscheinlichkeit durch aufgenommene Virionen ist kumulativ – vermutlich über acht Stunden. (...)
 • 2/2021 • Seite 24 • DPG-Mitglieder
• 2/2021 • Seite 24 • DPG-MitgliederWelche Auswirkungen hat die Covid-19-Pandemie auf die Work-Life-Balance?
Zwischen Mitte April und Ende Juni 2020 führte der Arbeitskreis Chancengleichhheit der DPG eine weltweit angelegte Online-Umfrage durch, um die Auswirkungen der Pandemie auf unsere Arbeit und unseren Alltag zu ermitteln.
Seit April 2020 sind 81 Prozent aller Arbeitskräfte weltweit aufgrund der Covid-19-Pandemie von obligatorischen oder empfohlenen Schließungen von Arbeitsplätzen betroffen. Laut dem Bericht des UN-Ausschusses für die Koordinierung statistischer Aktivitäten stellt dies den größten Beschäftigungsrückgang auf den Arbeitsmärkten seit dem Zweiten Weltkrieg dar.1)
Der Arbeitskreis Chancengleichheit (AKC) der DPG untersuchte in einer Umfrage die Lebensumstände, die Bedingungen bei der Fernarbeit (oder Homeoffice), die Herausforderungen an die Selbstorganisation, Führungsstil sowie Bedenken über die Zeit nach der Pandemie verschiedener demografischer, regionaler, Bildungs- und Berufsgruppen. Durch Fernarbeit verursachter Stress, die Veränderung der Lebensstile und unterschiedliche Vorstellungen über die Zeit nach der Pandemie standen dabei im Fokus. Die Ergebnisse der selbst gestalteten, anonymen Umfrage stehen online frei zur Verfügung.2) Die Analyse der Umfrage umfasst vollständige Antwortsätze von 1524 Teilnehmenden, die überwiegend aus Europa kamen (84 Prozent). 43 Prozent (663) der Teilnehmenden hatten einen Hintergrund in Physik, 70 Prozent (1061) haben eine akademische Position inne.
Ergebnisse
Alle Teilnehmergruppen zeigen ähnliche Muster in Bezug auf die Stressfaktoren. Das Fehlen von Urlaub, Wochenendunternehmungen, Aktivitäten mit Freunden und Familie, also der Wegfall der typischen Aktivitäten in einer Wohlstandsgesellschaft, führte zu Stress bzw. einer gesunkenen Lebensqualität. 812 bzw. 288 Teilnehmende bewerteten diese Auswirkungen als schwerwiegend bzw. mittel. (...)
 • 2/2021 • Seite 29 • DPG-Mitglieder
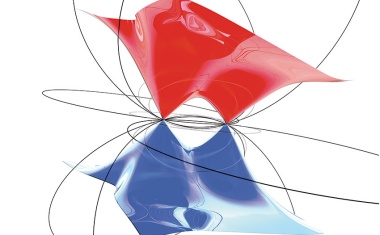
• 2/2021 • Seite 29 • DPG-MitgliederIn den letzten Jahren wurden viele neue topologische Materialien mit ungewöhnlichen Eigenschaften entdeckt, darunter auch Weyl-Halbmetalle.
Weyl-Halbmetalle sind topologische Materialien, die durch die Quantenzustände ihrer Elektronen an Kreuzungspunkten in ihrer Bandstruktur neuartige exotische Eigenschaften zeigen. An diesen Kreuzungspunkten verhalten sich die Leitungselektronen wie relativistische chirale Teilchen – sogenannte Weyl-Fermionen. Zuerst wurden diese in der Teilchenphysik vermutet, nun aber in Festkörpern gefunden.
Elektronische Eigenschaften von Festkörpern sind in unserem Leben allgegenwärtig. Sie bestimmen unter anderem die Farbe von Materialien und deren Festigkeit und werden in elektrischen Bauelementen nutzbar gemacht. Sie sind auch Grundlage zahlreicher Physik-Nobelpreise; prominente Beispiele sind die Hochtemperatur-Supraleitung (1987), der Riesenmagnetowiderstand (2007) oder Graphen (2010). Die elektronischen Eigenschaften von Festkörpern ergeben sich aus der Wechselwirkung von Elektronen mit den Atomen, aus denen der Festkörperkristall aufgebaut ist. Die Elektronen in einem Festkörper spüren die umliegenden Ionenrümpfe und können dadurch andere Eigenschaften besitzen als Elektronen im freien Raum.
Die Dispersionsrelation der Elektronen in einem Festkörperkristall, also die Relation der Energie mit dem Impuls, lässt sich durch das Bändermodell beschreiben, das in Bandstrukturdiagrammen darstellbar ist. Aus solchen Diagrammen sind unter anderem die Gesamtmasse der Elektronen und deren Geschwindigkeit im Festkörper abzulesen. Die einzelnen Bänder können mit Elektronen gefüllt bzw. besetzt (in den Abbildungen in diesem Artikel farbig dargestellt) oder leer bzw. unbesetzt sein. Die Fermi-Energie, welche die besetzten von den unbesetzten Zuständen trennt, bestimmt den „Füllstand“ der Elektronen in einem Festkörper. In geordneten Phasen, wie sie in Kristallen und Magneten vorliegen, legen vor allem Symmetrien die Form der Bandstruktur fest. Denn in einem Kristall sind die Ionen aufgrund ihrer elektrostatischen Wechselwirkungen periodisch angeordnet, wodurch die kontinuierliche Symmetrie des Raums unter Rotationen und Translationen gebrochen wird. Bei typischen Magneten ist zusätzlich ein Teil der Rotationssymmetrie zusammen mit der Zeitumkehrsymmetrie gebrochen. Ändert sich die Symmetrie des Festkörperkristalls, ändern sich folglich auch die Bandstruktur und damit die elektrischen und optischen Eigenschaften des Materials. (...)
 • 2/2021 • Seite 36 • DPG-Mitglieder
• 2/2021 • Seite 36 • DPG-MitgliederDie Dynamik von Quantensystemen kann im zeitlichen Verlauf selbstähnlich werden.
Die Zeitentwicklung isolierter Systeme ist auf kleinsten Skalen durch die Gesetze der Quantenmechanik bestimmt und kann sehr kompliziert ablaufen. Für große Systeme besteht in extrem dynamischen Situationen die Möglichkeit, dass die Zeitentwicklung einfach wird und universelles Verhalten zeigt. Analoge Quantensimulatoren helfen, dies zu untersuchen.
Systeme fernab des Gleichgewichts zeichnen sich durch eine typischerweise komplexe dynamische Entwicklung beobachtbarer Größen aus. Als „einfacher“ Spezialfall besitzen isolierte Quantensysteme eine Dynamik, die nur durch zwei Größen bestimmt wird: den Anfangszustand, z. B. in Form einer Dichtematrix, und den Hamilton-Operator. Daraus lässt sich mithilfe der Schrödinger-Gleichung bzw. der Von-Neumann-Gleichung die Zeitentwicklung bestimmen und so auch die dynamische Entwicklung aller beobachtbaren Größen. Dies erscheint konzeptionell sehr einfach, in der Praxis ist aber eine exakte Berechnung der Dynamik großer Systeme fast unmöglich.
In extremen Situationen kann die Dynamik jedoch einfach bzw. universell werden, beispielsweise im Quark-Gluon-Plasma. Für diesen heißesten Aggregatzustand auf Erden, produziert am CERN, schlägt die Theorie universelle Dynamik vor. Erstmals beobachtet wurde das Phänomen aber 2018 mit ultrakalten Bose-Gasen, dem kältesten Aggregatzustand auf Erden. Diese analogen Quantensimulatoren haben also beim Nachweis geholfen, dass universelle Quantendynamik in einer gegebenen physikalischen Situation auftritt. Im Folgenden wollen wir zunächst die Charakteristika der universellen Quantendynamik detaillierter betrachten.
Auf dem Weg zum Gleichgewicht
Um zu verstehen, was universelle Zeitentwicklung bedeutet, wollen wir uns zuerst einmal anschauen, wie sich eine Situation fernab des Gleichgewichts von einer nahe des Gleichgewichts unterscheidet. Im thermischen Gleichgewicht zeigt ein System keine explizite Zeitentwicklung. Die einzelnen Freiheitsgrade und deren Fluktuationen sind vollständig durch einen Parameter – die Temperatur – bestimmt. Daher folgen die Besetzungszahlen der Energiezustände, welche die Diagonalelemente der Dichtematrix sind, einer Boltzmann-Verteilung. Für den Spezialfall eines Bose-Kondensats ist der energetisch niedrigste Zustand makroskopisch besetzt, und die Besetzung der angeregten Zustände folgt der Bose-Einstein-Verteilung.
Für sehr lange Zeiten entwickeln sich die meisten Quantensysteme hin zu einem (thermischen) Gleichgewichtszustand, selbst wenn sie perfekt isoliert von der Umgebung sind. Wie genau generische isolierte Quantensysteme ein thermisches Gleichgewicht finden können, ist per se eine hochaktuelle Fragestellung. Wir interessieren uns hier speziell für die transiente Zeitentwicklung auf dem Weg zum thermischen Gleichgewicht, bei der universelle Quantendynamik auftreten kann. (...)
Die DPG-Schülertagungen 2020 haben Schülerinnen und Schüler in ganz Deutschland verbunden.
Das erste Online-Wochenendseminar der jungen DPG beschäftigte sich über einen Zeitraum von mehr als 40 Stunden hinweg mit der Zeit.
Die DPG macht in einem offenen Brief Vorschläge zur Klassenraumbelüftung.
Als Ergänzung zum GPT fand 2020 erstmals der Physikwettbewerb „Online-GPT 2020“ statt.