Eulers Rösselsprungrätsel
Alte Kreuzwort- und Zahlenrätsel besitzen interessante kombinatorische und topologische Problemstellungen zwischen Sprache und Wissenschaft.
„Über sieben Brücken mußt du gehn.“ Das bekannte Lied der DDR-Rockband Karat geht auf ein Gedicht in einem Roman von Helmut Richter zurück, der 1974 auf einer polnischen Legende basierend eine unglückliche Liebesgeschichte erzählte. Es geht um schwierige unklare Lebenswege, die überstanden werden müssen, und die Zahl 7 ist natürlich sinnbildlich. Der Ursprung von solchen Orakeln und Sprichwörtern ist oft unklar, auch Richter bezog sich nicht direkt auf das Königsberger Brückenrätsel.
Dieses Rätsel war für Leonard Euler 1736 Anlass, topologische Begriffe einzuführen, um die Unmöglichkeit einer Lösung mathematisch beweisen zu können. Das damals öffentlich diskutierte Rätsel bestand darin, ob man in Königsberg über alle sieben Brücken genau einmal gehen und wieder zum Ausgangspunkt zurückkehren kann. Euler formalisierte die Aufgabe mit dem neuen mimetischen Konzept eines „Graphen“, führte neue ekphratische Metaphern wie „Knotengrad“ ein. Damit zeigte er, dass in der Königsberger Topographie die Anzahl der Wege, die an einer Kreuzung zusammenkommen, gerade sein müssen, wenn ein geschlossener Weg glücken soll. Er schuf mit diesen Begriffen eine neue mathematische Disziplin, was zeigt, dass Mathematik auch Begriffsarbeit ist.
In der Antike wurden mythischen Orakelstätten wie Delphi die Autorenrolle für Weisheitssprüche zugeschrieben, aber vermutlich gehen sie auf eine kreative Sprachpraxis zurück, die Lebenserfahrung in Sprachbilder kondensierte. Gerade in sprachlichen Kleinformen wie Redewendungen („Fünfe gerade sein lassen“), Sprichwörtern („Es ist nicht alles Gold, was glänzt“) und Orakeln begegnet man frühen, undifferenzierten Vorformen der Wissenschaft.
Elementare Erfahrungen basieren oft auf grundlegenden mathematischen Strukturen wie der Unmöglichkeit einer „Quadratur des Kreises“ oder physikalischen Gesetzmäßigkeiten wie der Apfel, der nicht weit vom Stamm fällt. Deswegen finden auch physikalische Metaphern wie „Schwarzes Loch“ und „Quantensprung“ sowie geflügelte Worte wie „Gott würfelt nicht“ schnell Eingang in die Alltagssprache. Die enge Verwandtschaft von Redewendungen, Sprichwörtern und Orakeln mit wissenschaftlicher Erkenntnis sieht man unter anderem in der einfachen Form des Witzes, also einer fiktionalen Erzählung, die so strukturiert ist, dass eine überraschende Aufklärung eines vermeintlichen Problems zum Lachen anregt.
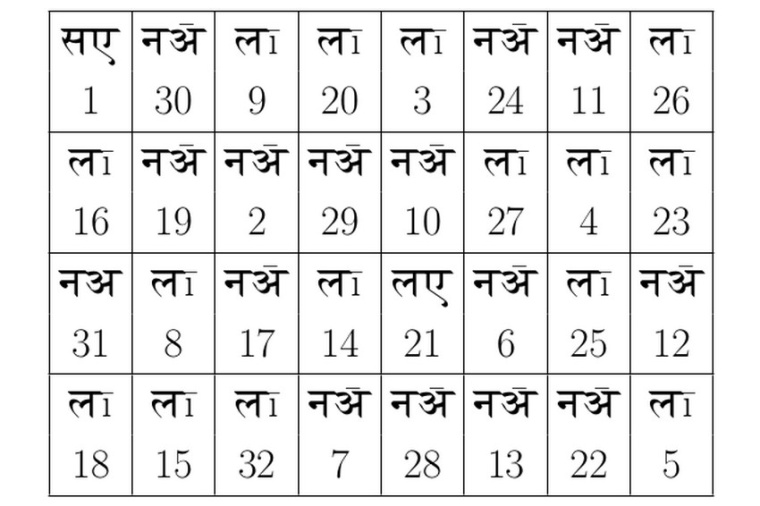
Auch bei Kreuzwort- und Zahlenrätsel gehen Sprache und Wissen eine enge Verbindung ein. Seit dem Mittelalter kennt man in Deutschland sogenannte „Rösselsprungrätsel“. Bei dieser Rätselart ist eine Fläche in quadratische Felder – oft 64 wie auf einem Schachbrett – eingeteilt, in der scheinbar wahllos Silben oder Buchstaben verteilt sind, die man durch die Züge eines Springers zu einem sinnvollen Satz ordnen soll. Diese Form der Literatur geht auf den persischen Dichter Rudrata zurück, der um 875 in seinem Hauptwerk Kavylankara ein 32-silbiges Gedicht in 4 Zeilen schrieb, das sowohl seriell von links nach rechts und von oben nach unten als auch entlang des Zuges eines Springers gelesen, denselben Spruch ergab. Sanskrit erleichtert eine solche literarische Akrobatik, da Wörter mehrere Bedeutungen haben und die Silben eines Worts auch verschieden kombiniert werden können.
Euler beschäftigte sich mit solchen literarischen Rätseln. 1759 zeigte er, dass es auf einem Schachbrett möglich ist, geschlossene Springerwege zu finden, die jedes Feld genau einmal besuchen. Er zeigte zudem, wie unvollständige Lösungen korrigiert und neue Lösungen aus bekannten generiert werden können. Heute weiß man, dass es immerhin 13 267 364 410 532 geschlossene Springerwege gibt.
Zwar war das Brückenproblem der Beginn der topologischen Argumentation, aber erst mit der Arbeit am literarischen Rösselsprungrätsel und seiner berühmten Elementa Doctrinae Solidorum von 1757 über seine Polyederformel hat Euler die neue Topologie signifikant ausgebaut. 1769 behauptete der Mechaniker Wolfgang von Kempelen, einen mechanischen Schachtürken konstruiert zu haben, der selbständig Lösungen für das Springerproblem finden könne. Bis heute gibt es wegen diesem Fake einer künstlichen Intelligenz die diskriminierende Redewendung „getürkt zu haben“.
Klaus Mecke, Uni Erlangen-Nürnberg